
МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ГОРНЫХ ПОРОД ПОД НАГРУЗКОЙ ЧИСЛЕННЫМИ МЕТОДАМИ, НО ПО АЛГОРИТМУ КЛЕТОЧНОГО АВТОМАТА



|
Шестопалов А.В. ( sinergo@mail.ru ) МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ГОРНЫХ ПОРОД ПОД НАГРУЗКОЙ ЧИСЛЕННЫМИ МЕТОДАМИ, НО ПО АЛГОРИТМУ КЛЕТОЧНОГО АВТОМАТА |
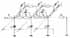
|

|
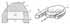
|
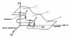
|

|

|
|

|