|
A.V.Shestopalov ( e_mail: sinergo@mail.ru )
SIMULATION OF ROCK BEHAVIOR UNDER LOAD USING NUMERICAL METHODS AND CELL AUTOMATON ALGORITHM
|
|
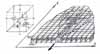
We suggest that a system of 4 bi-harmonic differential equations should be substituted for the cell automaton.
Mathematical model for the "coal seam-opening" system is generally reduced to solution of problems of fragile failure under three energy fluxes, i.e. rock pressure, filtrating gas pressure and loose mass weight pressure.
Appearance of internal sources for the last two fluxes may be jump-like only.
The solution algorithm says that function for the total pressure D(x,y) should be found at each iteration in the simulation area that satisfies the system of four biharmonic differential equations including an equation with pressure function D=F(Ô,P,G,x,y), where Ô, P and G are pressure functions of the remaining three equations in the above-mentioned system. Only one of the above listed functions may be present in one equation, x and y are space coordinates.
Each solution of every biharmonic equation consists of solutions of 2 Poisson harmonic equations according the same algorithm.
Final goal of the equation system solution analysis is to find coordinates of a cell (area) satisfying certain conditions that are the same for all cells. If the criterion is satisfied in some area, we change (e.g. decrease strength or increase gas permeability) properties of the medium and set internal sources for the respective pressure function.
Changes of boundary conditions in solution continuity area for all the 4 biharmonic equations precede solution of the mentioned equation system.
Self-organization of the front of the process under simulation happens during the solution spontaneously (by previously unknown inertia) as a result of identical non-linear (jump-like) changes in the simulated medium between the solutions.
© Institute of Complex Exploration of Mineral Wealth (IPKON RAN). Kryukovski Tupik, 4, Moscow, 111020, Russia, Tel. (+7 095)360-89-39, Fax (+7 095)360-89-60.
|