In English, please! Как доклады выглядели на стенде (второй из двух) Как доклады выглядели на стенде (первый из двух)

Шестопалов А.В.   A.V.Shestopalov         Программа

Моделирование поведения горных пород под нагрузкой численными методами, но по алгоритму клеточного автомата
Simulation of Rock Behavior under Load Using Numerical Methods and Cell Automaton Algorithm

- Доклад на Международной конференции "Компьютерное конструирование новых материалов и технологий" (Томск, Россия, 29-31 марта, 2001г.)
- Report of International Conference "CADAMT'2001" (March 29-31, 2001, Tomsk, Russia).



Уважаемые коллеги, дамы и господа.




Слайд 1 		Слайд 2
Слайд 3 Слайд 4
Слайд 5
Новой областью применения синергетики стала механика горных пород на больших глубинах, где начинает проявляться самопроизвольное разрушение краевой части горного массива (слайд 1).

Система "горный массив - выработка (полость)" - открытая система и, на больших глубинах, может быть сильно удалена от своего механического равновесия (слайд 2).

Процесс саморазрушения краевой части угольного пласта - это типичная задача синергетики (слайд 3).

Процесс саморазрушения распространяется от поверхности обнажения вглубь массива и продолжается до восстановления механического равновесия. Последнее достигается за счет образования области разупрочненного угля (слайд 4).

Если эту область уменьшить до критических размеров или уничтожить, то произойдет следующий скачок процесса саморазрушения до восстановления механического равновесия (слайд 5).

Слайд 6 Слайд 7
Слайд 8 Слайд 8
Образование зоны отжима в краевой части угольного пласта, нами интерпретируется как образование диссипативных структур (слайд 6).

При этом, описать словами эволюцию самоорганизующейся диссипативной структуры практически не возможно (слайд 7).

Для визуализации используем метод неподвижных клеточных автоматов (слайд 8).

Мы предлагаем заменить клеточный автомат системой из 4-х бигармонических дифференциальных уравнений, решение которых осуществляется численными методами, например методом конечных элементов (МКЭ), но по алгоритму клеточного автомата.

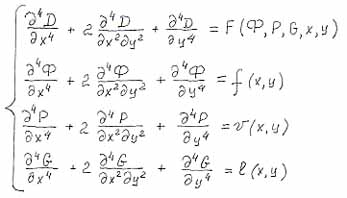
Система уравнений

Слайд 9
Область непрерывности решения (слайд 9) представляет собой полуплоскость с бесконечно удаленной границей D=100% напорной функции и границей в виде прямой линии D=0%.

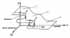
- суммарная (результирующая) напорная функция.


Граничные условия


Слайд 10
В общем случае математическая модель системы "угольный пласт - выработка" сводится к решению задач хрупкого разрушения под действием трех потоков энергии: горного давления, давления фильтрующегося газа и давления веса разуплотненной массы (слайд 10). Появление внутренних источников последних двух потоков может быть только скачкообразным.

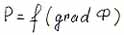
Давление свободного газа

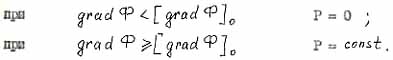
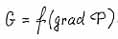
Давление веса разупрочненных горных пород (угля)

Слайд 11
Алгоритм решения предписывает (слайд 11), что на каждой итерации, в области моделирования, требуется найти функцию суммарного давления D(x, y), удовлетворяющей системе дифференциальных уравнений из 4-х бигармонических дифференциальных уравнений, одним из которых является уравнение с напорной функцией D=F(Ф, P, G, x, y), где Ф, P и G - напорные функции 3-х других уравнений, входящих в указанную систему уравнений. При этом в одном уравнении может быть только одна из перечисленных функций. x, y - пространственные координаты. Каждое решение каждого бигармонического уравнения состоит из решения 2-х гармонических уравнений Пуассона по тому же самому алгоритму.

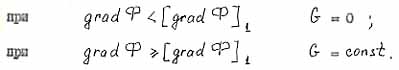
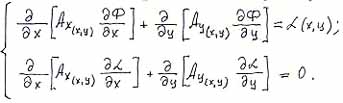
Деформирование под действием сил горного давления

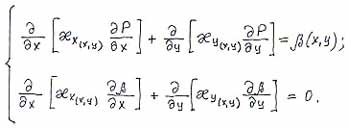
Деформирование под действием сил газового давления

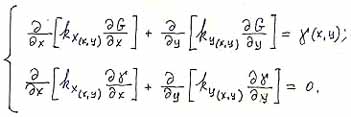
Деформирование под действием сил веса разупрочненной горной массы

Слайд 12
Конечной целью анализа решения системы уравнений является определение координат "клетки" (области), удовлетворяющей принятым, неизменным для всех "клеток", определенным условиям (слайд 12). При выполнении критерия в некоторой области, изменяем (например, уменьшаем прочностные свойства или увеличиваем газопроницаемость) свойства среды в этой области и задаем внутренние источники соответствующей напорной функции. Изменения граничных условий в области непрерывности решения всех 4-х бигармонических уравнений, предшествуют следующему решению указанной системы уравнений.

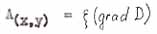
Прочностные свойства угля (породы)

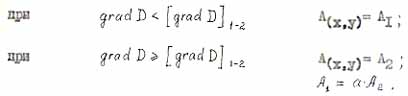
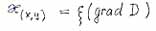
Фильтрационные свойства разупрочненной горной массы

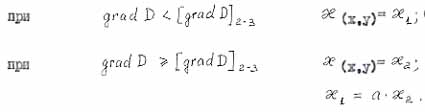
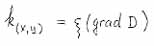
Внутреннее сцепление разупрочненной массы

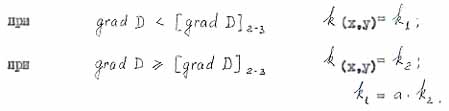
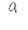
- безразмерный коэффициент (множитель) изменения кратности свойств геосреды при ее псевдофазовых переходах.

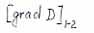
Шаг разупрочнения имеет минимум две критические величины:
- критерий псевдоплавления;
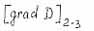
- критерий псевдокипения.


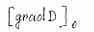
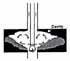
Слайд 13
Самоорганизация фронта моделируемого процесса в режиме обострения (слайд 13) возникает при решении спонтанно (на неизвестной заранее итерации) в результате идентичных нелинейных (скачкообразных) изменений свойств моделирующей среды между решениями. При этом, предполагается, что растущие трещины, при достижении фундаментальной длины, генерируют метан из угольного вещества, в результате чего газ и проницаемость появляются одновременно и скачкообразно.
При первом значении этой величины, на острие растущей трещины генерируется новое вещество (в данном случае метан). При втором значении этой величины, метана генерируется так много, что он не успевает фильтроваться в выработку, расклинивает трещину и становится сам причиной, вызывающей рост трещины.


Слайд 14 Слайд 15
При этом автор пытается доказать, что для системы "горный массив выработка", сильно удаленной от своего механического равновесия, справедливо следующее.
1. Хрупкое разрушение горных пород в виде трещин и пластическая деформация в металлах с образованием трещин - это одно и то же (слайд 14, 15).
2. Наличие или отсутствие концентраторов напряжений и др. прочностные свойства не влияют на внешний вид (характер - древовидность) системы трещин дальнего порядка.
3. Образование техногенных трещин саморазрушения в краевой части горного массива - это фрактал, как в смысле геометрии так и в смысле механизма процесса.
4. Краевая часть горного массива на больших глубинах - это могоуровневая самоорганизующаяся система техногенных трещин саморазрушения, в которой потеря сдвиговой устойчивости происходит самосогласованно на микро-, мезо-, макро- и мегомасштабных уровнях. Это приводит к возникновению диссипативных структур (фрагментации геоматериала) на перечисленных структурных масштабных уровнях.

Благодарю за внимание.




Вернуться на главную www.shestopalov.org Вернуться на главную sinergo.exponenta.ru
  ©   29.03.2001-19.08.2005    Шестопалов А.В.